Big-O en Español Parte 2
Expresiones cuadráticas y cómo se comportan las funciones elevadas a cualquier potencia en la notación Big-O.
En el post previo Big-O en Español Parte 1, revisamos la notación de Big-O para expresiones lineales y constantes. En este post vamos a explorar las expresiones cuadráticas y cómo se comportan las funciones elevadas a cualquier potencia.
Expresiones Cuadráticas
Vamos a ilustrar esta notación con un ejemplo práctico.
Supongamos que tenemos un arreglo con todas las selecciones de fútbol masculino que han salido campeonas del mundo desde 1930. Este arreglo incluye el nombre del país tantas veces como mundiales ganó:
const campeonesMundiales = ["Uruguay", "Italia", "Italia", "Uruguay", "Alemania",
"Brasil", "Brasil", "Inglaterra", "Brasil", "Alemania", "Argentina",
"Italia", "Argentina", "Alemania", "Brasil", "Francia",
"Italia", "España", "Alemania", "Francia"];Ahora supongamos que tenemos otro arreglo con todas las selecciones que participaron en el Mundial de Qatar 2022:
const seleccionesQatar = ["Qatar", "Alemania", "Dinamarca", "Brasil", "Francia",
"Paises Bajos", "Argentina", "Iran", "Corea del Sur", "Japon", "Arabia Saudita",
"Ecuador", "Uruguay", "Canada", "Ghana", "Senegal", "Marruecos", "Tunez", "Portugal",
"Polonia", "Camerun", "Mexico", "Estados Unidos", "Gales", "Australia", "Costa Rica"];Queremos averiguar cuáles de estas selecciones han sido campeonas del mundo y cuántas veces.
Código
El siguiente código realiza esta tarea:
function listarCampeones() {
for (let i = 0; i < seleccionesQatar.length; i++) {
const seleccion = seleccionesQatar[i];
let count = 0;
for (let j = 0; j < campeonesMundiales.length; j++) {
if (seleccion === campeonesMundiales[j]) {
count++;
}
}
console.log(`La selección ${seleccion} ${(count === 0 ? "no ha salido campeona del mundo" : `ha ganado ${count} mundial(es)`)}.`);
}
}En este código, por cada selección que participa en Qatar, verificamos cada entrada en el arreglo de campeones del mundo. Esto implica dos bucles anidados, lo que resulta en una complejidad cuadrática.
Complejidad Matemática
Cada bucle tiene una complejidad lineal O(n). Al combinarlos, obtenemos:
f(x) = x * x = x²Esto significa que el tiempo de ejecución crece proporcionalmente al cuadrado del tamaño de los arreglos. Cuanto más grandes sean los arreglos, más tiempo llevará procesar todas las combinaciones.
Expresiones Cúbicas y Potencias Mayores
Si añadimos más bucles anidados al algoritmo, seguimos multiplicando la complejidad lineal. Por ejemplo:
- Tres bucles anidados:
f(x) = x * x * x = x³- Cuatro bucles anidados:
f(x) = x * x * x * x = x⁴Representación Gráfica
A continuación, una gráfica que muestra cómo el tiempo de ejecución se incrementa con el tamaño de los datos en funciones cuadráticas y de mayor potencia:
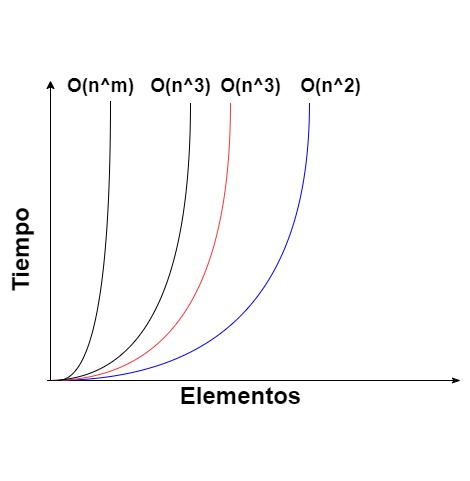
Como se observa, las potencias más altas hacen que el tiempo de procesamiento crezca de manera exponencial, lo que puede llevar a tiempos de ejecución inaceptables.
Recomendaciones
Para optimizar algoritmos con bucles anidados:
- Reducir bucles innecesarios: Evita iteraciones redundantes que puedan ser optimizadas.
- Usar estructuras de datos eficientes: Por ejemplo, emplear tablas hash puede reducir búsquedas lineales o cuadráticas a búsquedas constantes (O(1)).
- Dividir y conquistar: Algoritmos como quicksort y mergesort usan este enfoque para reducir la complejidad.
Conclusión
En este post, exploramos las expresiones cuadráticas y el impacto de las potencias mayores en la complejidad computacional. Estas notaciones son esenciales para identificar problemas de escalabilidad en algoritmos.
En la próxima parte, hablaremos de otros tipos de expresiones, como las logarítmicas, exponenciales y factoriales. ¡No te lo pierdas!